动态规划

yuanmoc2020/8/2大约 6 分钟

动态规划的定义

最优子结构（数学优化方法）
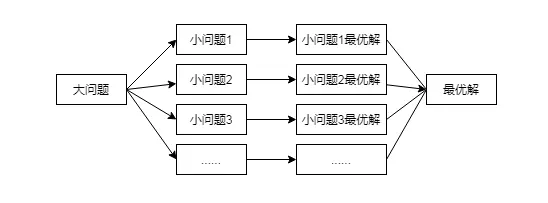
动态规划是数学优化的方法指，动态规划要解决的都是问题的最优解。而一个问题的最优解是由它的各个子问题的最优解决定的。

重叠子问题（编程方法）
动态规划是编程的方法指，可以借助编程的技巧去保证每个重叠的子问题只会被求解一次。

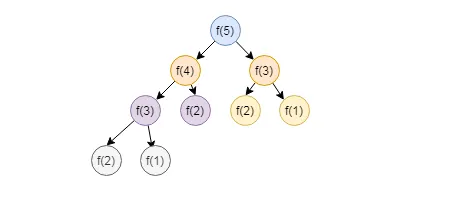
因此，判断一个问题能不能称得上是动态规划的问题，需要看它是满足这两个重要的属性：最优子结构（Optimal Substructure）和重叠子问题（Overlapping Sub-problems）。

动态规划方法

递归（Recursion）

递归的解法需要耗费非常多的重复计算，很多计算都是重叠的，可以使用记忆化的方法避免重叠计算问题。

记忆化（Memoization）

记忆化，就是将已经计算出来的结果保存起来，那么下次遇到相同的输入时，直接返回保存好的结果，能够有效节省了大量的计算时间。

自底向上（Bottom-Up）

自底向上指，通过状态转移方程，从最小的问题规模入手，不断地增加问题规模，直到所要求的问题规模为止。依然使用记忆化避免重复的计算，不需要递归。

斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

Java代码

// 递归的实现
public int fib(int n) {
    if(n <= 1){
        return n;
    }else{
        return fib(n-1)+fib(n-2);
    }
}

// 记忆化的实现
public int fib(int n) {
    // 用于记忆上一次的结果
    int[] fn = new int[n+1];
    fn[0] = 0;
    fn[1] = 1;
    for (int i = 2; i <= n; i++) {
        fn[i] = fn[i-1] + fn[i-2];
    }
    return fn[n];
}

// 自底向上的实现
public int fib(int n) {
   if(n <= 1) {
        return n;
   }
   int f0 = 0, f1 = 1, res = 0;
   for(int i = 2; i <= n; i++) {
        res = f0 + f1;
        f0= f1;
        f1= res;
   }
   return res;
}

动态规划面试题分类

线性规划

线性，就是说各个子问题的规模以线性的方式分布，并且子问题的最佳状态或结果可以存储在一维线性的数据结构里，例如一维数组，哈希表等。

解法中，经常会用 dp[i] 去表示第 i 个位置的结果，或者从 0 开始到第 i 个位置为止的最佳状态或结果。例如，最长上升子序列。dp[i] 表示从数组第 0 个元素开始到第i个元素为止的最长的上升子序列。

第一种形式，当前所求的值仅仅依赖于有限个先前计算好的值，也就是说，dp[i] 仅仅依赖于有限个 dp[j]，其中 j < i。

LeetCode 第 70 题

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

公式：f(x)=f(x−1)+f(x−2)

class Solution {
    public int climbStairs(int n) {
        if(n <= 2) {
            return n;
        }
        int f1 = 1, f2 = 2, res = 0;
        for(int i = 3; i <= n; i++) {
            res = f1+f2;
            f1=f2;
            f2=res;
        }
        return res;
    }
}

LeetCode第 198 题

第二种求解 dp[i] 的形式，当前所求的值依赖于所有先前计算好的值，也就是说，dp[i] 是各个 dp[j] 的某种组合，其中 j 由 0 遍历到 i−1。

LeetCode 第 516 题

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 ：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。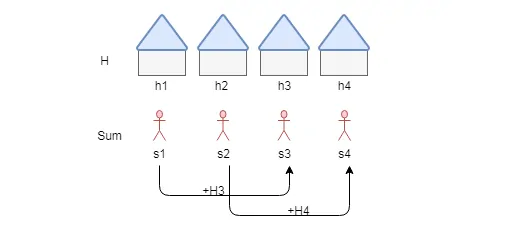

分析：
S 表示前S个房子能拿到的最大金额。
H 表示当前房子有多少钱。
第一间房：s1 = h1
第二间房：s2 = max(h1, h2)
第三间房：s3 = max(s1+h3, s2)
第四间房：s4 = max(s2+h4, s3)
第n间房：sn = max( s(n-2) +hn, s(n-1) )

class Solution {
    public int rob(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        int length = nums.length;
        if (length == 1) {
            return nums[0];
        }
        int f0= nums[0], f1= Math.max(nums[0], nums[1]);
        for (int i = 2; i < length; i++) {
            int temp = f1;
            f1= Math.max(f0+ nums[i], f1);
            f0= temp;
        }
        return f1;
    }
}

约束规划

在普通的线性规划和区间规划里，一般题目有两种需求：统计和最优解。
这些题目不会对输出结果中的元素有什么限制，只要满足最终的一个条件就好了。但是在很多情况下，题目会对输出结果的元素添加一定的限制或约束条件，增加了解题的难度。

0-1 背包问题

公式：

B(k, w) = max( B(k-1, w), B(k-1,w-wk) + Vk )

比较是放了第k个物品后价值大还是不放价值大。
k：前k个物品
w：还剩下多少容量，wk第k个物品重量
v：价值，Vk第k个物品价值
B(k-1, w)：是不放第k个物品
B(k-1,w-wk) + Vk：放了第k个物品

/**
 * 01背包问题
 * @param numOfItems 多少个商品
 * @param maxWeight 背包的容量
 * @param values 商品的价值
 * @param weights 商品的重量
 * @return 最在价值
 */
public int solution(int numOfItems, int maxWeight, int[] values, int[] weights) {
    int[][] tmp = new int[numOfItems+1][maxWeight+1];
    for (int i = 1; i <= numOfItems ; i++) {
        int value = values[i-1];
        int weight = weights[i-1];

        for (int j = 1; j <= maxWeight; j++) {
            if (j >= weight) {
                tmp[i][j] = Math.max(tmp[i-1][j], tmp[i-1][j-weight] + value);
            } else {
                tmp[i][j] = tmp[i-1][j];
            }
        }
    }
    return tmp[numOfItems][maxWeight];
}

NP 完全问题

该例题为 NP 完全问题。NP 是 Non-deterministic Polynomial 的缩写，中文是非決定性多项式。通俗一点来说，对于这类问题，我们无法在多项式时间内解答。这个概念很难，但是理解好它能帮助你很好的分析时间复杂度。

多项式级别时间复杂度
O(1)、O(n)、O(n×logn)、O(n2)、O(n3) 等，可以表示为 n 的多项式的组合

非多项式级别时间复杂度
O(2n)，O(3n) 等指数级别和 O(n!) 等阶乘级别

END!