堆排序

堆定义
每个堆都是完全二叉树（从上到下，从左到右，高最大相差一）。
大顶堆：每个结点的值都大于或等于其左右孩子结点的值。
小顶堆：每个结点的值都小于或等于其左右孩子结点的值。

image.png

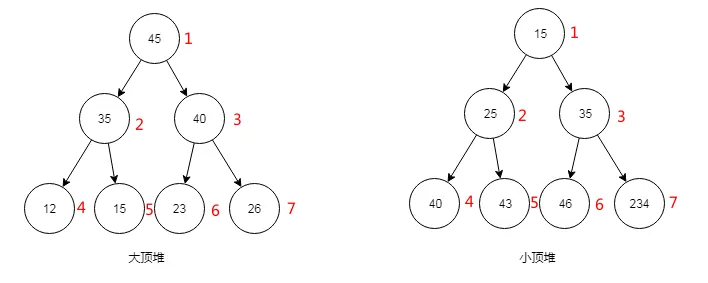
同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子。

整体解题思路：
1、先把要排序的数据放到数组中。
2、对数组中的数组进行构建成堆。
3、将构建好的堆中的头数据与结尾数据交换并截取出结尾数据。
4、继续将剩下的数据构建成堆，并重复3操作，直到结束。

构建成堆时的几个关键点：
1、尾部元素的父结点计算： (arr.length-1)/2
2、父元素的左结点计算：i * 2 + 1
3、父元素的右结点计算：i * 2 + 2
4、从右到左，从下到上进行比较与交换，最后形成堆

Java代码

public class HeapSort {

    public static void main(String[] args) {

        int[] arr = {16, 2,123,7, 3, 20, 17, 8,123,1,221};
        HeapSort heapSort = new HeapSort();
        heapSort.heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public void heapSort(int[] arr) {
        // 找出大头堆，与结尾交换，并截取出尾部
        for (int i = arr.length-1; i > 0; i--) {
            // 将交换后的数组，再次构建成堆
            buildHeap(arr,i);
            swap(arr,0, i);
        }
    }

    /**
     * 构建堆
     *      10
     *     /  \
     *    5    8
     *   / \  / \
     *  3  4 6  7
     *  正好可以用一个数组表示 {10,5,8,3,4,6,7}
     *  元素父节点： (i-1)/2
     *  元素左子节点： 2i+1
     *  元素右子节点： 2i+2
     * @param arr 数组
     * @param length 堆长度
     */
    private void buildHeap(int[] arr, int length) {
        // 父节点
        int parent = (length - 1) / 2;
        for (int i = parent; i >= 0 ; i--) {
            adjustHeap(arr, i, length);
        }
    }

    /**
     * 调整堆，，找出最大值节点，与parent节点交换
     * @param arr 数组
     * @param parent 父节点
     * @param length 堆长度
     */
    private void adjustHeap(int[] arr, int parent, int length) {
        int leftChild = 2 * parent + 1;
        int max = parent;

        // 左节点
        if (leftChild <= length && arr[leftChild] > arr[max]) {
            max = leftChild;
        }
        // 右节点
        if (leftChild + 1 <= length && arr[leftChild + 1] > arr[max]) {
            max = leftChild + 1;
        }
        if (max != parent) {
            swap(arr, max, parent);
        }
    }

    private void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

}