图深度、广度优先遍历
图的种类
1、无向图(Undirected Graph):每个顶点和其他顶点通过相连线连接。
2、有向图(Drirected Graph):有向图中的相连线是有方向的。
3、权重图(Weighted Graph):在权重图中,每条相连线各自有各自的权重。
有向图的实现
1、矩阵
使用矩阵来表示图之间的连向关系,用一个一维数组来保存顶点,再二维数组来保存顶点之间的关联。如:
1->2有关联,就在edge[1][2]=1来表示。
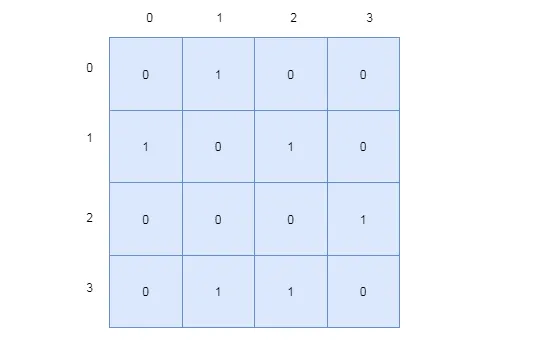
2、链表
用链表来表示两个顶点之间的关系,用一维数组来保存各个顶点,再以顶点为头节点,关联边用链表串起来。如:
0->1有关联,就用一条链表保存起来。
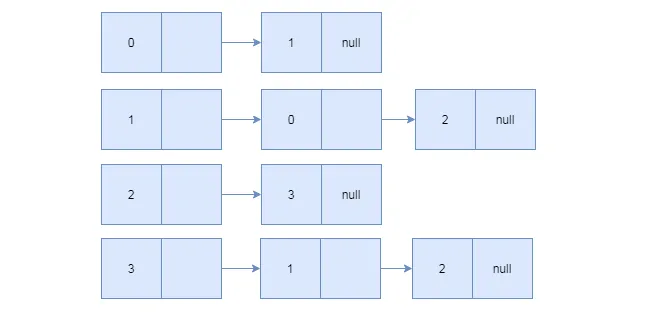
DFS与BFS过程
深度优先算法主要与栈有关(先进后出),广度优先算法与堆有关(先进先出)。
深度优先算法
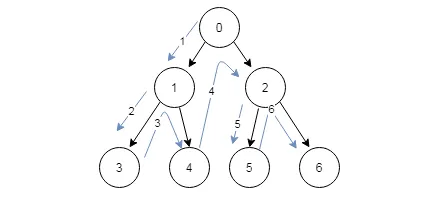
过程:
1、先将0放在栈中
栈中数据:0
打印数据:
2、0出栈并打印,把0相关联的放入栈中,即把1、2放入栈中
栈中数据:1、2
打印数据:0
3、1出栈并打印,把1相关联的放入栈中,即把3、4放入栈中
栈中数据:3、4、2
打印数据:0、1
4、3出栈并打印,3没有相关联的了,就没有数据入栈
栈中数据:4、2
打印数据:0、1、3
5、4出栈并打印,4没有相关联的了,就没有数据入栈
栈中数据:2
打印数据:0、1、3、4
6、2出栈并打印,把2相关联的放入栈中,即把5、6放入栈中
栈中数据:5、6
打印数据:0、1、3、4、2
7、5出栈并打印,5没有相关联的了,就没有数据入栈
栈中数据:6
打印数据:0、1、3、4、2、5
8、6出栈并打印,6没有相关联的了,就没有数据入栈
栈中数据:
打印数据:0、1、3、4、2、5、6
9,栈中没有数据,结束。
广度优先算法
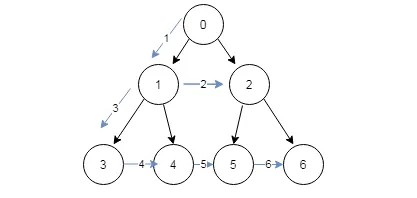
过程:
1、0放入堆中
堆中数据:0
打印数据:
2、0出堆并打印,把与0相关联的1、2放入堆中
堆中数据:2、1
打印数据:0
3、1出堆并打印,把与1相关联的3、4放入堆中
堆中数据:4、3、2
打印数据:0、1
4、2出堆并打印,把与2相关联的5、6放入堆中
堆中数据:6、5、4、3
打印数据:0、1、2
5、3出堆并打印,因为没有相关联的,所以没有数据放入堆中
堆中数据:6、5、4
打印数据:0、1、2、3
6、3出堆并打印,因为没有相关联的,所以没有数据放入堆中
堆中数据:6、5
打印数据:0、1、2、3、4
7、3出堆并打印,因为没有相关联的,所以没有数据放入堆中
堆中数据:6
打印数据:0、1、2、3、4、5
8、3出堆并打印,因为没有相关联的,所以没有数据放入堆中
堆中数据:
打印数据:0、1、2、3、4、5、6
9、堆中没有数据,结束。
Java代码
对有向图进行深度优先和广度优先搜索。
public class Graph {
/**
* 顶点数组
*/
Vertex[] vertexList;
/**
* 用于保存顶点边
*/
int[][] edges;
/**
* 最大顶点个数
*/
int maxVertexNum;
/**
* 顶点个数
*/
int vertexNum;
/**
* 顶点类
*/
class Vertex {
/**
* 顶点标识
*/
char label;
/**
* 是否已经访问过
*/
boolean wasVisited;
public Vertex(char label) {
this.label = label;
wasVisited = false;
}
}
public Graph(int maxVertexNum) {
this.maxVertexNum = maxVertexNum;
vertexNum = 0;
vertexList = new Vertex[maxVertexNum];
edges = new int[maxVertexNum][maxVertexNum];
}
/**
* 加入顶点
* @param label 顶点标识
*/
public void addVertex(char label) {
if (vertexNum > maxVertexNum) {
throw new IndexOutOfBoundsException("加入元素比最超过最大容量");
}
vertexList[vertexNum++] = new Vertex(label);
}
/**
* 添加边
* @param from 开始元素
* @param to 指向元素
*/
public void addEdge(int from, int to) {
edges[from][to] = 1;
}
/**
* 重置顶点被访问标识
*/
public void reset() {
for (int i = 0; i < vertexList.length; i++) {
vertexList[i].wasVisited = false;
}
}
/**
* 打印顶点
* @param vertex 顶点
*/
public void print(Vertex vertex) {
System.out.print(vertex.label + " ");
}
/**
* 深度优先算法
*/
public void depthFirstSearch() {
// 放顶点数组索引
Stack<Integer> stack = new Stack<>();
// 添加首节点
stack.add(0);
while (!stack.isEmpty()) {
// 出栈,打印,并设置元素被访问过
Integer pop = stack.pop();
print(vertexList[pop]);
vertexList[pop].wasVisited = true;
// 添加相关联节点
for (int i = 0; i < edges[pop].length; i++) {
if (edges[pop][i] == 1 && !vertexList[i].wasVisited) {
stack.add(i);
}
}
}
reset();
}
/**
* 广度优先算法
*/
public void breadthFirstSearch() {
// 放顶点数组索引
Queue<Integer> queue = new LinkedList<>();
// 添加首节点
queue.offer(0);
while (!queue.isEmpty()) {
// 出队列,打印,并设置被访问过
Integer poll = queue.poll();
print(vertexList[poll]);
vertexList[poll].wasVisited = false;
// 添加相关联节点
for (int i = 0; i < edges[poll].length; i++) {
if (edges[poll][i] == 1 && !vertexList[i].wasVisited) {
queue.add(i);
}
}
}
reset();
}
/**
* 测试图示例如下:
* -------------------
* | B -> C |
* | ^ |
* | | |
* | A -> D -> E |
* -------------------
*/
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addEdge(0,1);//AB
graph.addEdge(1,2);//BC
graph.addEdge(0,3);//AD
graph.addEdge(3,4);//DE
System.out.println("深度优先搜索算法:");
graph.depthFirstSearch();
System.out.println();
System.out.println("---------------");
System.out.println("广度优先搜索算法:");
graph.breadthFirstSearch();
}
}END!
